JPEG结构及编码解码
为什么会想到看这个东西呢,因为选了个数据恢复的课不得不了解一下(早知道就应该选水点的实验课了)
或许后面还会造个轮子玩玩吧。。
JPEG文件格式
JPEG文件通常以FFD8头部标识,以FFD9作为结束标识,在文件中以FF表示一个段的开头,后跟标识信息表示段的内容,再之后是两字节的数表示段的长度
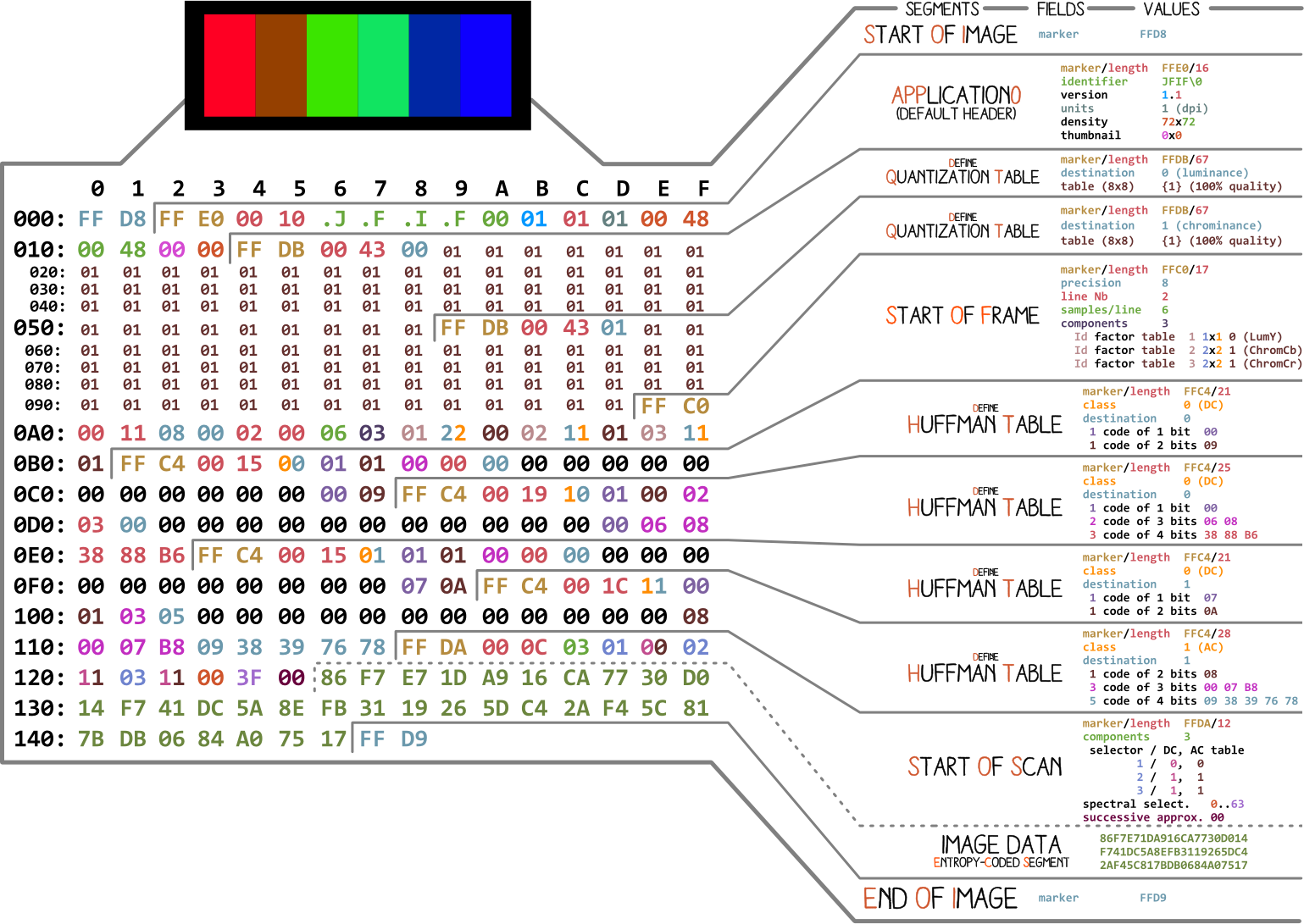
编码过程
色彩空间
大多数JPEG算法的实现使用亮度和色度(YUV编码)而非RGB编码,因为人眼很难观察到高频亮度在很小的区域中的变化。RGB使用3个字节来存储颜色信息,而YUV也使用3个字节来存储,但是每个字节表示的信息和RGB相比是不同的。图片的编码流程如下
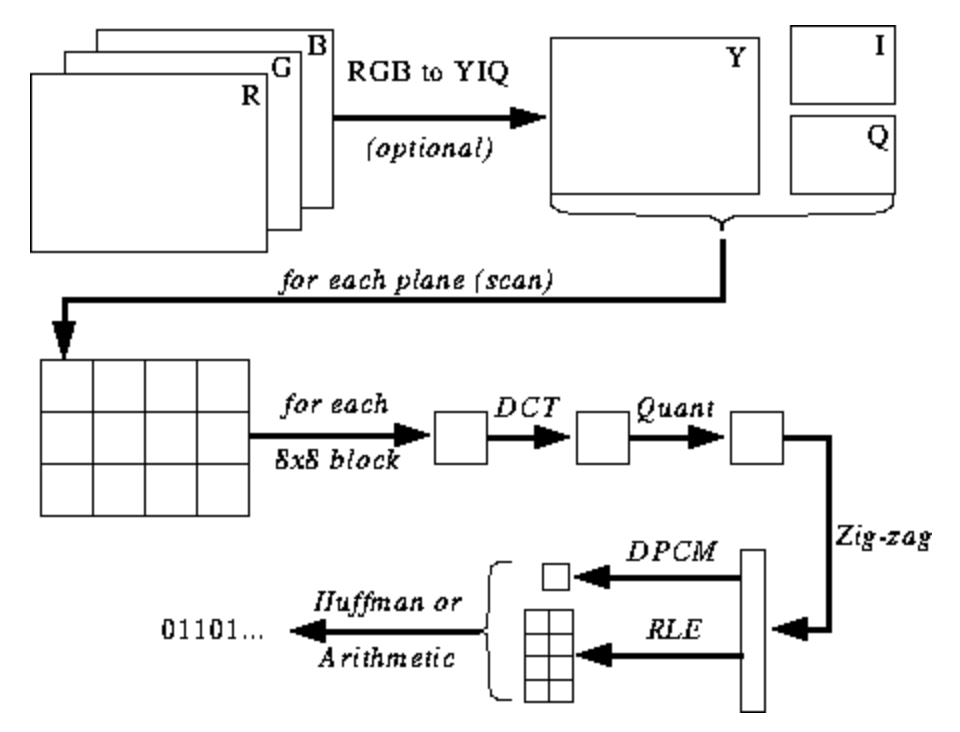
离散变换和量化
JPEG在处理图像之前将图片划分为8x8的小块来进行处理(这样的小块被称为最小编码单元),在处理的时候需要将像素值的范围进行修改,使得值的范围在$[-127, 128]$之间,未进行处理的范围在$[0, 255]$,使得像素值以0为中心,便于利用离散余弦变换。离散余弦变换把离散的数据变成多个余弦信号的组合。
二维DCT变换
二维DCT的变换公式:
$$
F(u,v) = c(u)c(v)\sum_{i = 0}^{N - 1}\sum_{J = 0}^{N - 1}f(i, j)cos[\frac{(i + 0.5)\pi}{N}]cos[\frac{(j + 0.5)\pi}{N}]
$$
$$
c(x) =
\begin{cases}
\sqrt{\frac{1}{N}}, x = 0 \\\
\sqrt{\frac{2}{N}}, x \neq 0 \\\
\end{cases}
$$看起来不太看得懂,但是主要注重怎么用就行了
将上面的式子改为矩阵的形式,令$U(i, j) = c(i)cos[\frac{(j + 0.5)\pi}{N}]$,则$F = UAU^T$,DCT矩阵$U$在8x8的方阵中如下
$$
U=\frac{1}{2}\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\\
cos\frac{\pi}{16} & cos\frac{3\pi}{16} & cos\frac{5\pi}{16} & cos\frac{7\pi}{16} & cos\frac{9\pi}{16} & cos\frac{11\pi}{16} & cos\frac{13\pi}{16} & cos\frac{15\pi}{16} \\\
cos\frac{2\pi}{16} & cos\frac{6\pi}{16} & cos\frac{10\pi}{16} & cos\frac{14\pi}{16} & cos\frac{18\pi}{16} & cos\frac{22\pi}{16} & cos\frac{26\pi}{16} & cos\frac{30\pi}{16} \\\
cos\frac{3\pi}{16} & cos\frac{9\pi}{16} & cos\frac{15\pi}{16} & cos\frac{21\pi}{16} & cos\frac{27\pi}{16} & cos\frac{33\pi}{16} & cos\frac{39\pi}{16} & cos\frac{45\pi}{16} \\\
cos\frac{4\pi}{16} & cos\frac{12\pi}{16} & cos\frac{20\pi}{16} & cos\frac{28\pi}{16} & cos\frac{36\pi}{16} & cos\frac{44\pi}{16} & cos\frac{52\pi}{16} & cos\frac{60\pi}{16} \\\
cos\frac{5\pi}{16} & cos\frac{15\pi}{16} & cos\frac{25\pi}{16} & cos\frac{35\pi}{16} & cos\frac{45\pi}{16} & cos\frac{55\pi}{16} & cos\frac{65\pi}{16} & cos\frac{75\pi}{16} \\\
cos\frac{6\pi}{16} & cos\frac{18\pi}{16} & cos\frac{30\pi}{16} & cos\frac{42\pi}{16} & cos\frac{54\pi}{16} & cos\frac{66\pi}{16} & cos\frac{78\pi}{16} & cos\frac{90\pi}{16} \\\
cos\frac{7\pi}{16} & cos\frac{21\pi}{16} & cos\frac{35\pi}{16} & cos\frac{49\pi}{16} & cos\frac{63\pi}{16} & cos\frac{77\pi}{16} & cos\frac{91\pi}{16} & cos\frac{105\pi}{16} \\\
\end{bmatrix}
$$
通过该矩阵进行相乘即可得到进行DCT处理后的信息矩阵
量化
在得到DCT矩阵后通过量化表来进行量化,量化的过程很简单,通常是根据压缩的精细度使用不同的量化表,DCT矩阵和量化表矩阵中对应位置的值进行相处得到量化后的矩阵。
编码&压缩
Zig-Zag
在量化完成之后,高频的位置的矩阵信息通常就变成0了,所以为了方便压缩,通过Z形扫描,将这些为0的值连到一起
例如:
$$
\begin{bmatrix}
15 & 14 & 10 & 9 \\\
13 & 11 & 8 & 0 \\\
12 & 0 & 0 & 0 \\\
0 & 0 & 0 & 0
\end{bmatrix}
$$
在经过扫描后,变成了
$$
\begin{bmatrix}
15 & 14 & 13 & 12 &11 & 10 & 9 & 8 &0 & …… & 0
\end{bmatrix}
$$
行程编码和增量编码
行程编码其实是一种较为容易想出来的压缩编码方式(突然想起来这个好像以前听卡常狂魔wys讲过orz)
行程编码简单来说就是统计当前信息连续出现多少次,并且记录次数
$$
\begin{bmatrix}
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{bmatrix}
$$
在进行编码后就是
$$
\begin{bmatrix}
0 & 8
\end{bmatrix}
$$
没记错的话那个时候听讲座还提到过这个压缩方式被哪家压缩软件的软件公司给申请了专利(?
然后增量编码是通过与之前的字节进行比较增量变换进行编码的方式
$$
\begin{bmatrix}
10 & 11 & 12 & 13 & 10 & 9
\end{bmatrix}
$$
在经过编码之后就是
$$
\begin{bmatrix}
10 & 1 & 2 & 3 & 0 & -1
\end{bmatrix}
$$
在JPEG中,DCT系数矩阵中的值都相对于前面的DCT表中的DC值进行了增量编码,这样可以让后面的DC值都能够靠近0,便于后续进行哈夫曼编码。所以如果修改图像的第一个DC系数会导致整个图片发送很大的变动,而修改靠后的DC系数引起的变化比较小。
In JPEG, every DC value in a DCT coefficient matrix is delta encoded relative to the DC value preceding it. This means that if you change the very first DCT coefficient of your image, the whole image will get screwed up but if you modify the first value of the last DCT matrix, only a very tiny part of your image will be affected. This is useful because the first DC value in your image is usually the most varied and by applying the Delta encoding we bring the rest of DC values close to 0 and that results in better compression in the next step of Huffman Encoding.
——《Understanding and Decoding a JPEG Image using Python》
哈夫曼编码
哈夫曼编码的实现这里不细说,JPEG里面通过哈夫曼编码压缩的方式将信息进一步压缩
在经过DCT变换以及量化后得到的DCT系数矩阵中,第一个数为DC系数,其他的63个为AC系数
对于亮度和色度需要进行不同的编码,而对应AC系数和DC系数也有不同的编码,所以一般来说一个彩色的JPEG图像中存在4个哈夫曼表
写一下哈夫曼表在JPEG中的存储形式,随便选了一张图片,哈夫曼表段如下

选取中间比较长的一段来进行说明
1 | Offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
FF C4表示哈夫曼表的开始,00 4B表示长度,随后跟的10表示类型,属于AC表的0号表
哈夫曼表的表类型:
高4位标识表示该表是AC交流表还是DC直流表,0表示DC,1表示AC
低4位标识表示该表是0号表还是一号表
主要看深蓝色部分和绿色部分
1 | 00 02 02 01 03 02 03 06 04 02 07 06 05 03 01 09 |
每个字节表示对应位数的码字的数量,例如位数为2、3、6、10的码字都有2个,而位数为3、16的码字都有1个等等,总的加起来就算后面剩余部分的长度(哈夫曼树的叶子节点的个数)
剩余部分根据码字长度表来依次建立,得到哈夫曼编码表,这里写前面一小部分
| 序号 | 码字长度 | 码字 | 值 |
|---|---|---|---|
| 1 | 2 | 00 | 0x00 |
| 2 | 2 | 01 | 0x01 |
| 3 | 3 | 100 | 0x02 |
| 4 | 3 | 101 | 0x11 |
| …… | …… | …… | …… |
中间码字缺失的,在当前码字加1后,补0到最后进行补足
解码
(咕咕咕)






